There are several underused and not-so-popular frameworks hidden in the iOS SDK. Some of them can be useful and time-saving tools. The Accelerate Framework is one of them. Available in both Swift and Obj-C, the Accelerate Framework is used to make large-scale mathematical and image calculations much easier for developers and optimized for high performance tasks. As a result it is used extensively in machine learning programs. This framework contains a variety of C APIs for vector and matrix math, digital signal processing, large number handling, and image processing. If that sounds complicated to you, don’t be worried. You don’t need to know much of the math behind it- just as long as you understand the concepts.
To begin, let’s go to Xcode and create a new playground. Name the playground whatever you want and set the platform to macOS. Once the playground is created, select everything and delete it. This way you’ll have a clean slate to work on. At the top of the playground, type the following to import the following libraries.
import Cocoa
import Accelerate
import simd
Now we are ready to begin writing code with the Accelerate framework!
BLAS (Basic Linear Algebra Subroutines)
In the first example we’ll be looking at how to solve a common linear algebra equation:
Ax + y
where “A” is a constant and x & y are matricies. If you don’t know what matrices or vectors are, don’t worry. A matrix is basically an array of numbers while a vector is a matrix with either 1 column or 1 row. So to begin, first we need to define our vectors.
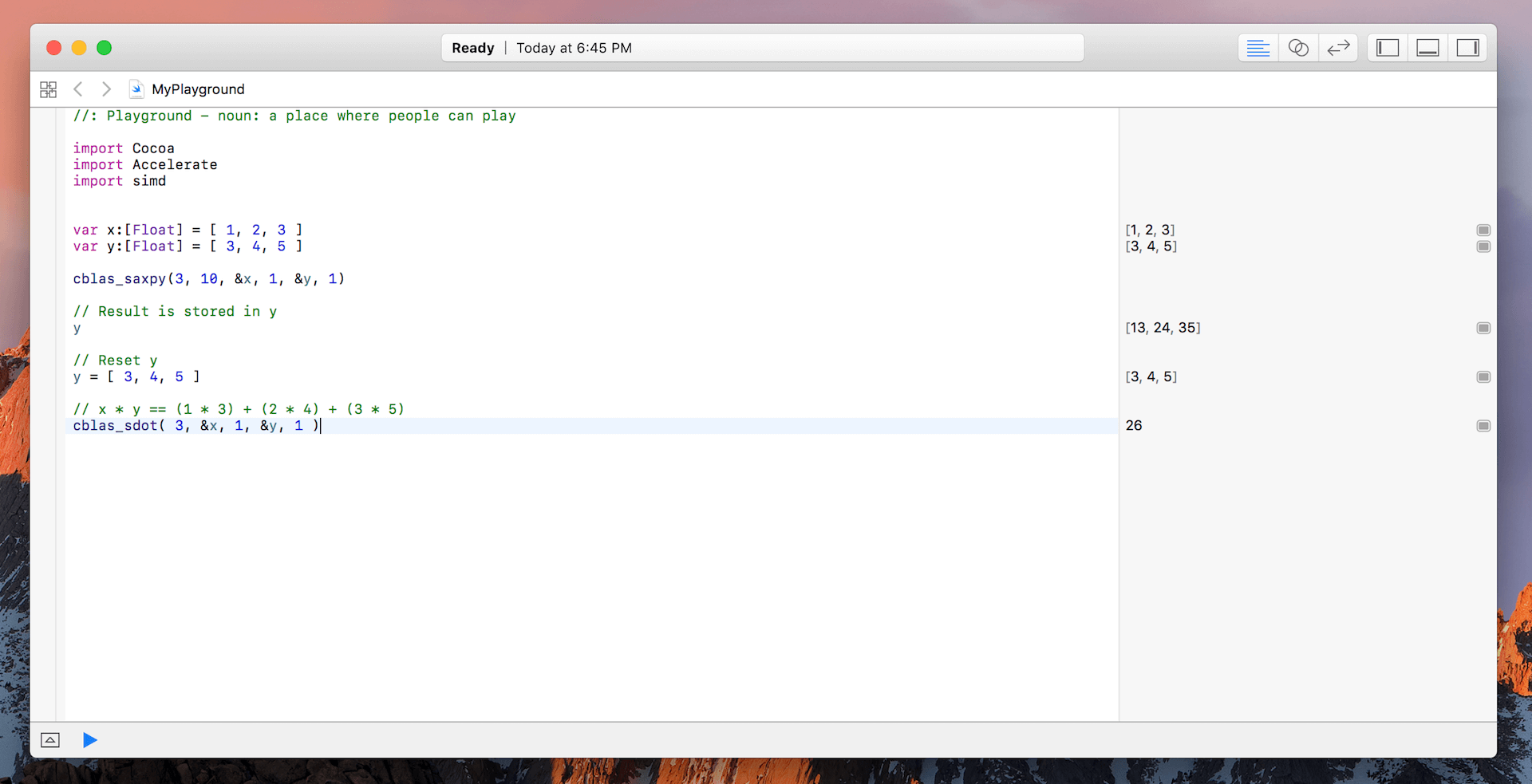
var x:[Float] = [ 1, 2, 3 ]
var y:[Float] = [ 3, 4, 5 ]
In the above code, we have defined our vectors x and y, with numbers 1, 2, & 3 and 3, 4, & 5 respectively. Now that we have our vectors x & y, let’s define our constant. For this example, I’ve decided to use 10 but you can use any number. So we are going to calculate this:
10x + y
Now copy the function given below.
cblas_saxpy(3, 10, &x, 1, &y, 1)
The function cblas_saxpy(_:_:_:_:_:_:) is a function which computes a constant times a vector plus a vector. This is exactly what we want. The parameters define (in order):
- the number of elements in the vector
- the constant A
- the “x” vector
- the stride in the “x” vector (For example if incX is 7, every 7th example is used)
- the “y” vector
- the stride in the “y” vector.
In the second example, we’ll be using the dot product to multiply vectors:
∑a[i] * b[i]
We’ll be using the same vectors from the previous example. Let’s reset y to what it was originally. Then we’ll multiply both vectors using the function cblas_sdot(_:_:_:_:_:).
y = [ 3, 4, 5 ]
// x * y == (1 * 3) + (2 * 4) + (3 * 5)
cblas_sdot( 3, &x, 1, &y, 1 )
The parameters of this function are similar to the cblas_saxpy(_:_:_:_:_:_:) function. The only difference is that there is no parameter for a constant since we are multiplying 2 vectors. For more functions in the BLAS library, you can look at them here.
LAPACK (Linear Algebra Package)
LAPACK isn’t really a standard Apple-issued library with the Accelerate framework but Swift supports it. This is a good thing because LAPACK has many advantages. In the next example, we will be solving simultaneous equations. The 3 equations we will be solving are:
- 7x+5y-3z = 16
- 3x-5y+2z= -8
- 5x+3y-7z= 0
Copy the following code into your playground.
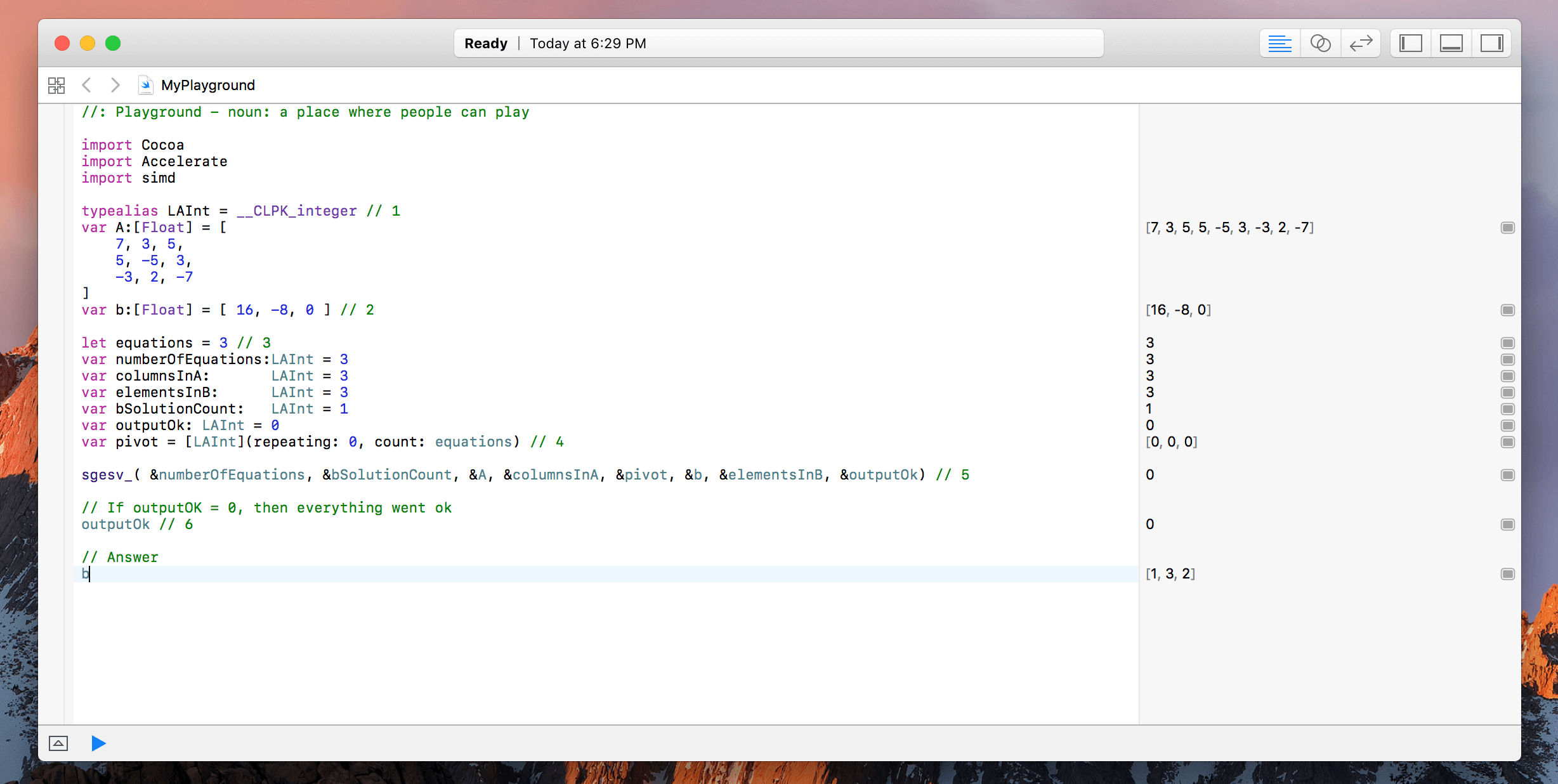
typealias LAInt = __CLPK_integer
var A:[Float] = [
7, 3, 5,
5, -5, 3,
-3, 2, -7
]
var b:[Float] = [ 16, -8, 0 ]
let equations = 3
var numberOfEquations:LAInt = 3
var columnsInA: LAInt = 3
var elementsInB: LAInt = 3
var bSolutionCount: LAInt = 1
var outputOk: LAInt = 0
var pivot = [LAInt](repeating: 0, count: equations)
sgesv_( &numberOfEquations, &bSolutionCount, &A, &columnsInA, &pivot, &b, &elementsInB, &outputOk)
// If outputOK = 0, then everything went ok
outputOk
// Answer
b
Let’s go through the code and see what’s going on!
- Line #1 – We are defining a type LAInt to use with our equations below.
- Line #7: Now, we are defining matrix A and vector B which will hold the constants that are in our simulataneous equations. Matrix A will hold the constants on the left hand side of the equation and Vector B will hold the constants on the right hand side of the equations.
- Line #9: We define the number of simultaneous equations we are going to solve.
- Line #15: Now, we define a number of variables which will be put into the parameters of the
sgesv_(_:_:_:_:_:_:_:_:)subroutine. - Line #17: We perform the
sgesvsubroutine. The parameters define (in order): the number of linear equations to solve, the number of columns in vector B, the coefficient matrix A, the columns in matrix A, the permutation matrix, the coefficient vector B, the columns in vector B, and the outputOK. - Line #20: This variable determins if the calculations went ok. If outputOk = 0, then the calculations were successful, otherwise the equations couldn’t be soved.
If all the calculations went right, then when you type b, the output should be [1, 3, 2]. These are the solutions for x, y, & z.
simd (Single Instruction Multiple Data)
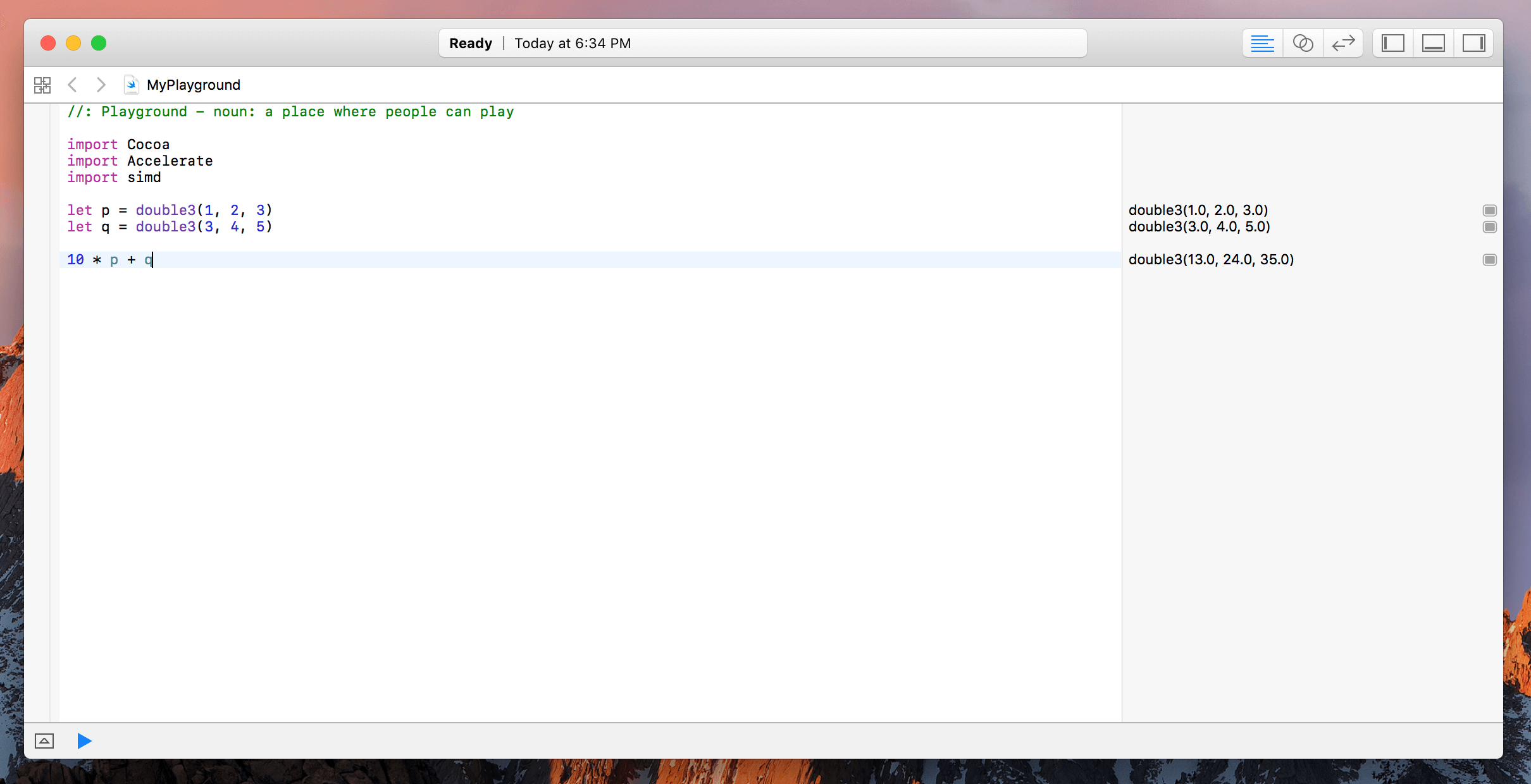
simd is also another library outside of the Accelerate framework, yet compatible with Swift. This library also simplifies many mathematical compuattions. Remember the the first example in BLAS where we had to use the cblas_saxpy(_:_:_:_:_:_:) function? Well there is an even easier way to perform the computation:
10 * x + y
To avoid the overlapping of variables, let’s change x & y to p & q. First, brgin by defining vectors p and q.
let p = double3(1, 2, 3)
let q = double3(3, 4, 5)
Now… here’s the magic:
10 * p + q
That’s it! This was much easier than using cblas_saxpy(_:_:_:_:_:_:). While this example was relatively simple, simd is more commonly used in 2D, 3D, and 4D math and geometry. It also works great with other libraries such as ModelIO, SpriteKit, Metal, etc. However, since the math is way too complex for this tutorial, it won’t be covered.
vecLib (Single Instruction Multiple Data)
vecLib is a library which contains functions which can abstract the vector processing library. If you are using vector instructions in your app, it is recommended that you use these functions so that your code can output to different CPU architecture. Let’s begin by copying the following code where we just define a function for creating a Float array:
func floats(_ n: Int32) -> [Float] {
return [Float](repeatElement(0, count: Int(n)))
}
Now in the first example, we will be calculating the absolute values of a vector. For example, if I define a vector A = [-3, -2, -5, -10], after is goes through the function, the vector should read [3, 2, 5, 10]. The function which we will use to accomplish this computation is vvfabsf(_:_:_:).
Now the first thing to do is to define the parameters. The parameters we will need are an integer containing the number of elements in each set, an input array, and an output array.
var count: Int32 = 4
var aAbsolute = floats(count)
var a:[Float] = [-3, -2, -5, -10]
Now that we have our parameters defined, there’s only one thing left to do: Plug it in!
vvfabsf(&aAbsolute, &a, &count)
aAbsolute
If all works well, you should get [3, 2, 5, 10] as your output!
In the second example, we’ll be truncating the numbers in a vector by using the vvintf(_:_:_:) function. Copy and paste the code into your playground:
count = 3
var f:[Float] = [3.3796, 1.8036, -2.1205]
var bInt = floats(count)
vvintf(&bInt, &f, &count)
bInt
Similar to the previous example, we begin by defining the parameters which are the same as the vvfabsf function. Then, we simply plug it in!
Now here’s a small challenge for you! Can you find the square roots of 16, 9, 4, and 1 by putting them in a vector, using the vvsqrtf(_:_:_:) function, and defining the parameters?
I hope you were able to complete the challenge! For those of you who couldn’t, don’t worry! This is really advanced stuff so it’s ok if you couldn’t get it on the first try.
Here is how you would find the square roots of 16, 9, 4, and 1.
count = 4
var c:[Float] = [16,9,4,1]
var cSquareRoots = floats(count)
vvsqrtf(&cSquareRoots, &c, &count)
cSquareRoots
The ouput for cSquareRoots should be [4, 3, 2, 1].
Now for the final example in vecLib: Can you take the inverse of a vector containing 4 fractions, [1/3, 2/5, 1/8, -3/1], if the function for taking an inverse is vvrecf(_:_:_:)? The parameters are the same as the previous examples.
I hope you were able to accomplish this. The code for accomplishing the computation is given below:
count = 4
var d:[Float] = [1/3, 2/5, 1/8, -3/1]
var dFlipped = floats(count)
vvrecf( &dFlipped, &d, &count )
dFlipped
These 4 examples were just a quick glance at the possibility of using vecLib in your apps. There are many more functions which you can use to accomplish your mathematical needs. For more functions and subroutines available in the vecLib Library, take a look at Apple Developer’s official vecLib documentation.
vDSP
vDSP is a library which has C and Swift APIs for performing common routines on a single vector. Similar to the previous libraries, you can perform matrix and vector arithmetic with this library… but I think you’ve had enough with that. So let’s try something different this time. Let’s say you have a set of points describing a path. How far are we from the origin at each step? It’s very easy to solve this with vDSP because we have several distance functions in the vDSP library!
Let’s start by defining several points on a NSBezierPath.
var points:[CGPoint] = [
CGPoint(x: 0, y: 0),
CGPoint(x: 0, y: 10),
CGPoint(x: 0, y: 20),
CGPoint(x: 0, y: 30),
CGPoint(x: 0, y: 40),
CGPoint(x: 0, y: 50),
CGPoint(x: 0, y: 60),
CGPoint(x: 0, y: 70),
CGPoint(x: 0, y: 80)
]
let path = NSBezierPath()
path.move(to: points[0])
// IMP: Remove the space between the < and points
for i in 1..< points.count {
path.line(to: points[i])
}
Notice how our points are all on the y-axis. This is so that when we mentally verify the calculations later on, it will be easier for us. Now, the function which we will be using for calculating the distance is vDSP_vdist(_:_:_:_:_:_:_:). The parameters define: the x-values, the stride in x, the y-values, the stride in y, the output vector, the stride for the output vector, and the numebr of elements to process.
var xs = points.flatMap { Float($0.x) }
var ys = points.flatMap { Float($0.y) }
var distance = [Float](repeating: 0, count: points.count)
vDSP_vdist(&xs, 1, &ys, 1, &distance, 1, vDSP_Length(points.count))
distance.map { $0 }
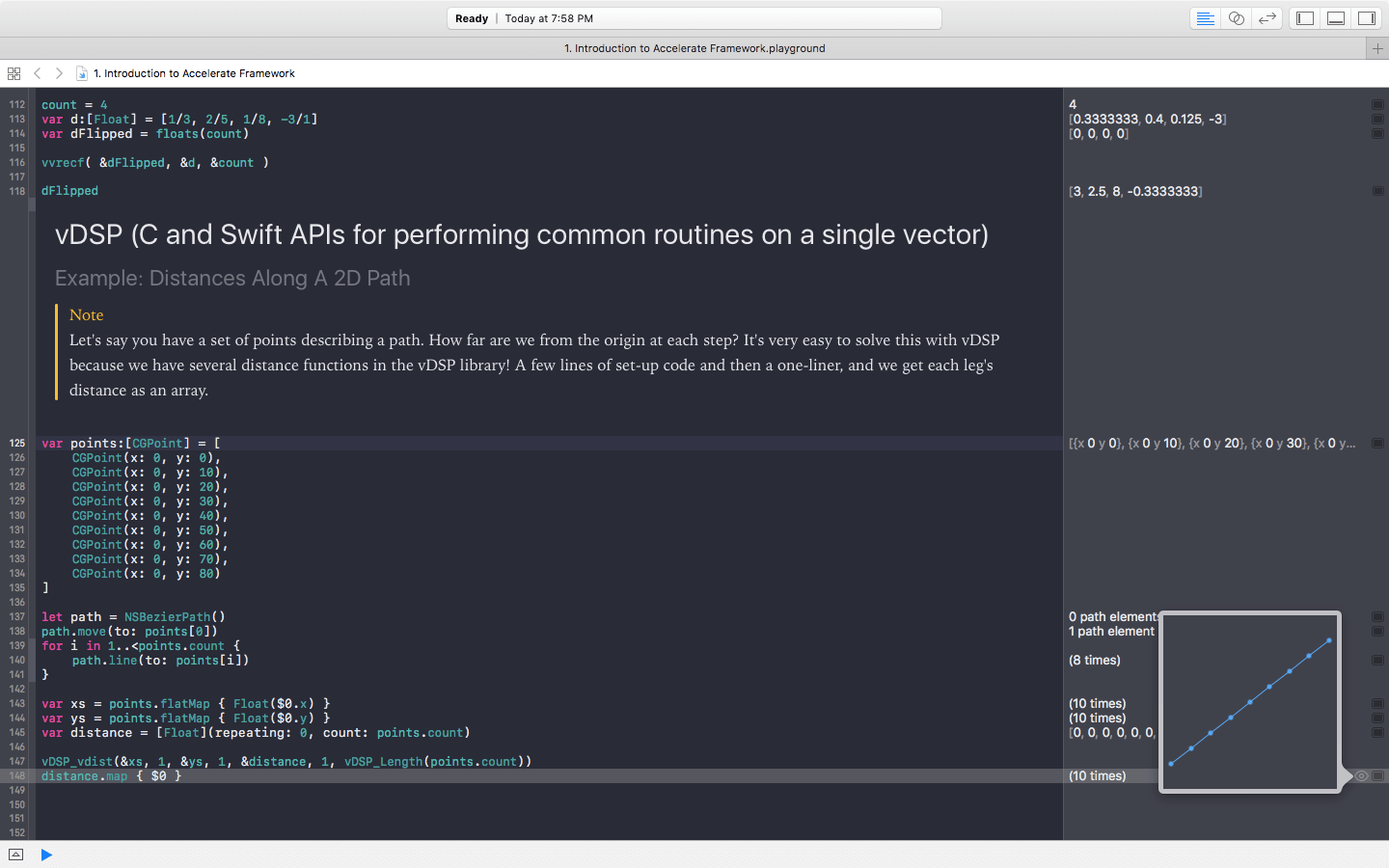
Now, it's hard to check if we are right... but bear with me. If you notice our points, at each point we add 10 to the origin and the number before it. So in an ascending order, our distance would be 10, 20, 30... and so on. Thus, since we are increasing by the same constant, if we were to plot these points we would get a linear graph. If you click on the little eye icon next to (10 times) in the output console, you should get something like this.
What if we wanted to calculate the entire distance traveled? Well that would just be 10 + 20 + 30 + blah blah blah. We're programmers... we don't want to mentally calculate this all the way to 80. NO! We write code so the computer can do the hard work for us and give us the correct output. To calculate the total distance, just type the following code.
distance.reduce(0, +)
And that's it! You should get 360 as an output!
Wrap Up
That's all I'm covering about Accelerate in this tutorial. This is a majority of the math in Accelerate. There are still 2 more important libraries: BNNS (Basic Neural Network Subroutines) and vImage (Vector calculations on images). However, if I had to cover them in this tutorial, it would never end. Plus, I think we all have had enough math for today. We'll talk about the other libraries later.
For reference, you can refer to the complete Xcode playground on GitHub.
For more details about the Accelerate framework, you can refer to the official Accelerate documentation.








